**타원 곡선 암호(ECC)**는 기존 방식보다 작고 빠르며 효율적인 것으로 유명한 데이터 암호화를 위한 키 기반 기술입니다. ECC는 웹 트래픽의 복호화 및 암호화를 위한 공개 키와 개인 키 쌍에 중점을 둡니다. ECC는 리베스트-샤미르-애들먼(RSA) 암호화 알고리즘과 관련하여 자주 논의됩니다.

개요

암호화에는 크게 두 가지 유형이 있습니다. 암호화와 복호화에 하나의 키를 사용하는 대칭 암호화(예: AES)와 두 개의 다른 키를 사용하는 비대칭 암호화(예: RSA)입니다. 이를 종종 공개 키와 개인 키라고 하며, 개인 키는 공개되지 않습니다. RSA는 대수적 수론에 기반한 정수 인수 분해 암호화를 사용하는 반면, 타원 곡선 암호(ECC)는 타원 곡선에 기반한 정수 인수 분해 암호화를 사용합니다. 타원 곡선 암호는 유한 필드에 대한 타원 곡선을 기반으로 하는 공개 키 암호화 방식입니다.^[2] ECC는 유사한 RSA 시스템에서 사용하는 리소스의 약 90%를 잠재적으로 절약할 수 있기 때문에 비트코인에서 암호화 키 알고리즘으로 사용됩니다.^[3]

RSA 대 ECC

ECC와 RSA는 모두 공개 키와 개인 키를 생성하고 두 당사자가 안전하게 통신할 수 있도록 합니다. 그러나 ECC의 한 가지 장점은 ECC의 256비트 키가 RSA를 사용하는 3072비트 키와 거의 동일한 보안을 제공한다는 것입니다. ECC를 사용하면 스마트폰, 임베디드 컴퓨터 및 암호화폐 네트워크와 같은 리소스 제약 시스템에서 RSA에 필요한 저장 공간 및 대역폭의 약 10%를 사용할 수 있습니다.

RSA

데이터를 암호화하는 데 사용하는 키는 공개할 수 있지만 데이터를 해독하는 데 사용되는 키는 비공개로 유지할 수 있다는 아이디어를 기반으로 합니다. 따라서 이러한 시스템은 공개 키 암호화 시스템으로 알려져 있습니다. 이러한 시스템 중 최초이자 여전히 가장 널리 사용되는 시스템은 RSA로 알려져 있습니다. 이 알고리즘을 처음 공개적으로 설명한 세 사람인 Ron Rivest, Adi Shamir 및 Leonard Adleman의 머리글자를 따서 명명되었습니다. RSA 알고리즘과 Diffie-Hellman 키 교환 알고리즘이 모두 도입되었을 때 이러한 새로운 알고리즘은 보안이 수론 이론에 기반한 최초의 실행 가능한 암호화 체계를 나타내기 때문에 혁신적이었습니다. 공유 비밀 없이 두 당사자 간의 안전한 통신을 가능하게 한 최초의 알고리즘이었습니다. 암호화는 비밀 코드북을 전 세계로 안전하게 운송하는 것에서 키 교환을 듣는 사람이 있는지 걱정하지 않고 두 당사자 간의 안전한 통신을 할 수 있는 것으로 바뀌었습니다.

ECC

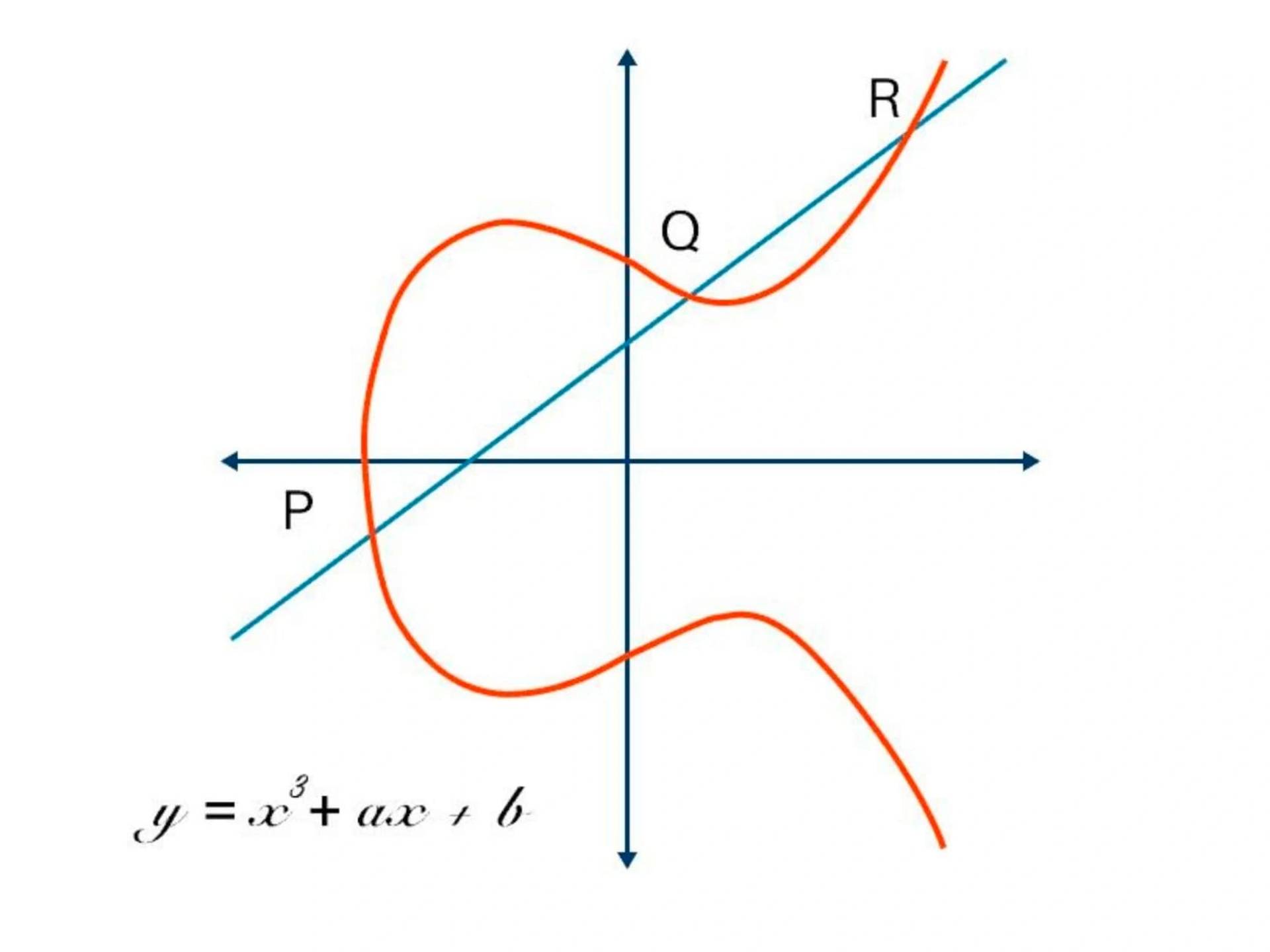
RSA 및 Diffie-Hellman이 도입된 후 연구자들은 훌륭한 트랩도어 함수 역할을 할 인수 분해 외에 다른 알고리즘을 찾기 위해 다른 수학 기반 암호화 솔루션을 탐색했습니다. 1985년에는 타원 곡선이라는 난해한 수학 분야를 기반으로 암호화 알고리즘이 제안되었습니다. 타원 곡선은 특정 수학 방정식을 충족하는 점들의 집합이며, 옆으로 기울어진 룰루레몬 로고와 약간 비슷하게 보입니다.

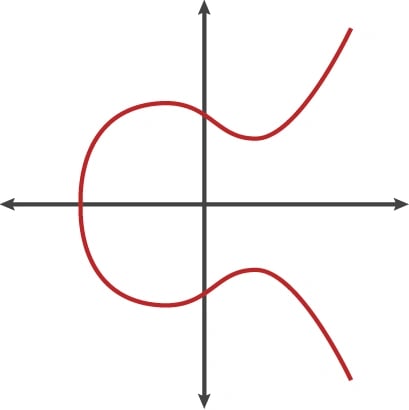
타원 곡선의 다른 표현도 있지만 기술적으로 타원 곡선은 변수 중 하나에서 2차이고 다른 변수에서 3차인 두 변수의 방정식에서 방정식을 충족하는 점들의 집합입니다. 타원 곡선에는 암호화에 적합한 몇 가지 속성이 있습니다.^[4]

제작자

Neal Koblitz와 Victor Miller는 오늘날 인터넷에서 암호화된 통신을 가능하게 하는 수학의 일부인 타원 곡선 암호화를 독립적으로 공동 발견했습니다. 2019년 All About Circuits(AAC)와의 인터뷰에서 Koblitz 박사는 다음과 같이 말했습니다.^[1]

"수론에 대한 제 생각을 바꾼 것은 1977년경에 RSA 암호화(Rivest-Shamir-Adleman)가 발명된 것입니다. 그것은 수론이 컴퓨터 보안에 적용된 최초의 중요한 사례였습니다." "타원 곡선 암호화의 아이디어는 1984년에 나왔습니다. 저는 다른 여러 사람들과 함께 Hendrik Lenstra가 큰 정수를 인수 분해하기 위해 개발한 알고리즘의 예비 버전인 사전 인쇄물을 받았습니다. 이 알고리즘이 충분히 빠르면 RSA 암호화에 위협이 될 수 있습니다."