有向无环图（DAG）是一种图数据结构，由通过有向边连接的节点组成，其中边具有特定方向且不形成任何环。它是一种没有有向环的有向图。

DAG 中的每个节点可以有一个或多个传入边和一个或多个传出边。DAG 中的边表示节点之间的依赖关系，其中边的方向表示依赖关系的方向。例如，如果节点 A 有一个指向节点 B 的传出边，则表示节点 A 依赖于节点 B。

概述

有向无环图 (DAG) 与 区块链 的不同之处在于它们不使用基于块的结构。相反，交易表示为图中的顶点，并链接到之前的交易。节点验证交易并将其添加到 DAG，提交交易需要完成 工作量证明 任务。^[1]

在基于 DAG 的网络中，新的交易必须引用之前的交易才能被接受，类似于区块链中的区块引用之前的区块。引用交易会确认它，并且为了使交易得到完全确认，它需要被后续交易引用。^[1]

由于没有区块创建且没有交易费用（因为没有矿工），DAG 具有很高的交易速度，这可能具有环境效益。^[2]

DAG 在某种意义上优于区块链，因为它们允许更高的吞吐量，通过结合区块链、工作量证明 和 权益证明 的概念，以及最长链规则与有向无环图。

历史

DAG 的首次使用日期不确定，但这个概念非常有用，可以追溯到人类存在的初期。

Leonhard Euler 于 1736 年发表的《柯尼斯堡七桥问题》被认为是第一篇涵盖图论的论文。柯尼斯堡七桥问题是数学史上一个著名的问题。挑战在于找到一条路线，只穿过柯尼斯堡（现在的俄罗斯加里宁格勒）的七座桥梁一次。在将城市地图简化为图后，Euler 介绍了他的公式，该公式与边、顶点和面的数量有关。

从这里开始，图论发展成为对对象之间关系的研究，用数学结构来描述。有许多不同类型的图，都有特定的定义，而 DAG 就是其中之一。^[3]

用例

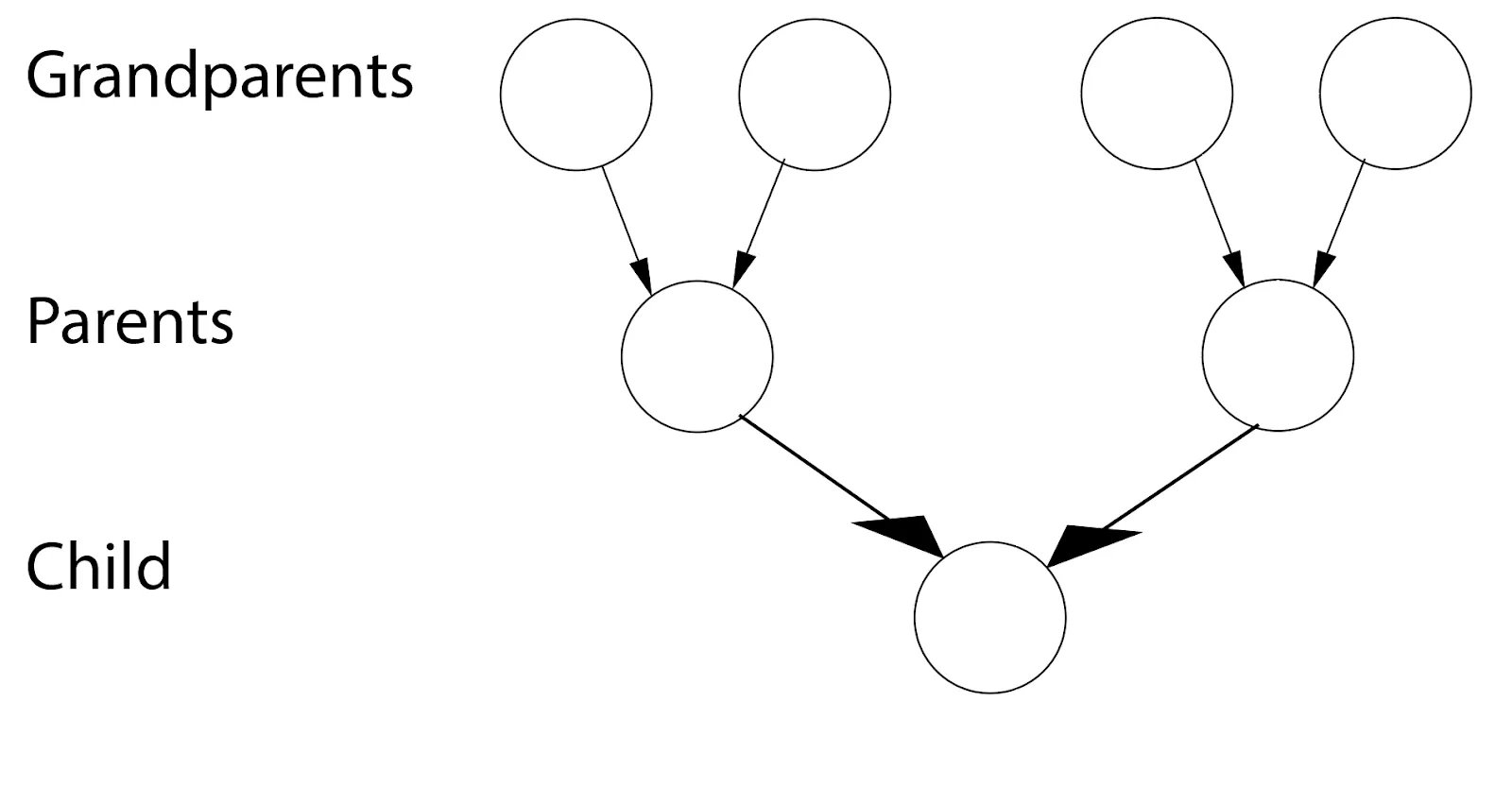
家谱

DAG 的一个原始用例是创建家谱。有趣的是，图论中树的定义不包括大多数家谱。这是因为在大多数追溯到足够远的家谱中，远房亲戚在某个时候已经交配，从而允许在家庭的父系和母系方面都有一个共同的祖先。这意味着，家谱可以被认为是一个 DAG——其中每个节点是一个人，每个亲子关系都画成一个指向后代的箭头。这形成了一个如下图所示的图，它是定向的（箭头）和无环的（没有人可以成为自己的父母）。

将家谱描绘成 DAG 的记录可以追溯到古罗马，老普林尼描述了装饰罗马贵族房屋墙壁的图。在此之前，DAG 可能没有被记录下来，但在解释家族历史时经常被描述。^[3]

任务调度

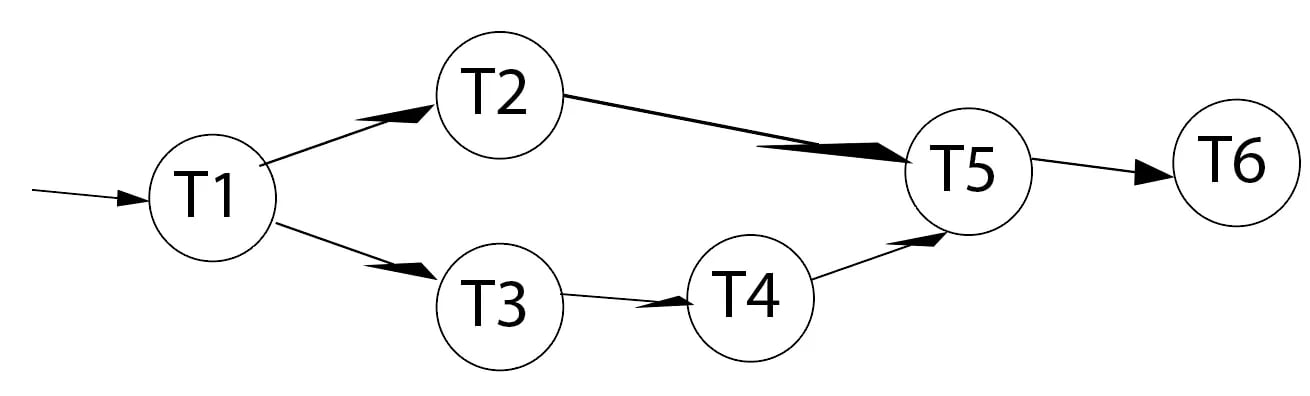
DAG 的另一个历史用例是任务调度，动物和人类天生就使用 DAG 来计算完成任务的顺序。有些任务只有在其他任务完成后才能开始，而其他任务可以随时开始——这本身就是一个 DAG。

在上面的 DAG 中，T1 可能是决定猎杀哪种动物作为晚餐，任务 2 是猎杀动物，任务 3 可以同时进行的是收集柴火。任务 4 是开始生火。任务 5，烹饪动物，需要火燃烧和动物被猎杀，任务 6 是吃晚餐，这需要先烹饪动物。类似（但更复杂）的 DAG 将用于任何大型任务，例如建造金字塔、设计罗马、计划战争中的攻击等。^[3]

计算机科学

DAG 的其他用例更加现代，与计算机科学相关的用途很多。数据处理网络、版本历史和一些数据压缩算法都利用了 DAG。但需要注意的是，DAG 并不是一个新的启示，而是一种古老的解决问题的机制。DAG 和 区块链 的合并是 分布式账本 可扩展性的一大进步。^[3]