椭圆曲线密码学 (ECC) 是一种基于密钥的数据加密技术，以其比现有技术更小、更快、更高效而闻名。ECC 侧重于公钥和私钥对，用于解密和加密网络流量。ECC 经常在 Rivest-Shamir-Adleman (RSA) 密码算法的背景下讨论。

概述

主要有两种不同的加密类型 - 对称加密，它使用一个密钥来加密和解密（例如 AES），以及非对称加密，它使用两个不同的密钥（例如 RSA）。这些通常被称为公钥和私钥，其中私钥不应被泄露。 RSA 使用基于代数数论的整数分解密码学，而椭圆曲线密码学 (ECC) 使用基于椭圆曲线的整数分解密码学。 椭圆曲线密码学是公钥密码学的一种选择，它基于有限域上的椭圆曲线。^[2] ECC 被用作比特币中的密码密钥算法，因为它有可能节省与类似 RSA 系统相比约 90% 的资源。^[3]

RSA 与 ECC

ECC 和 RSA 都生成公钥和私钥，并允许双方安全地通信。然而，ECC 的一个优势是，ECC 中的 256 位密钥提供的安全性与使用 RSA 的 3072 位密钥大致相同。ECC 允许资源受限的系统（如智能手机、嵌入式计算机和加密货币网络）使用 RSA 所需的约 10% 的存储空间和带宽。

RSA

基于这样的想法：任何人用来加密数据的密钥都可以公开，而用于解密数据的密钥可以保密。因此，这些系统被称为公钥密码系统。其中第一个也是目前使用最广泛的系统被称为 RSA——以首次公开描述该算法的三位男士的首字母命名：Ron Rivest、Adi Shamir 和 Leonard Adleman。 当 RSA 算法和 Diffie-Hellman 密钥交换算法被引入时，这些新算法是革命性的，因为它们代表了第一个可行的密码方案，其安全性基于数论。它是第一个实现双方之间安全通信而无需共享密钥的方案。 密码学从安全地在世界各地运输秘密密码本，发展到能够在任何两方之间进行安全通信，而无需担心有人监听密钥交换。

ECC

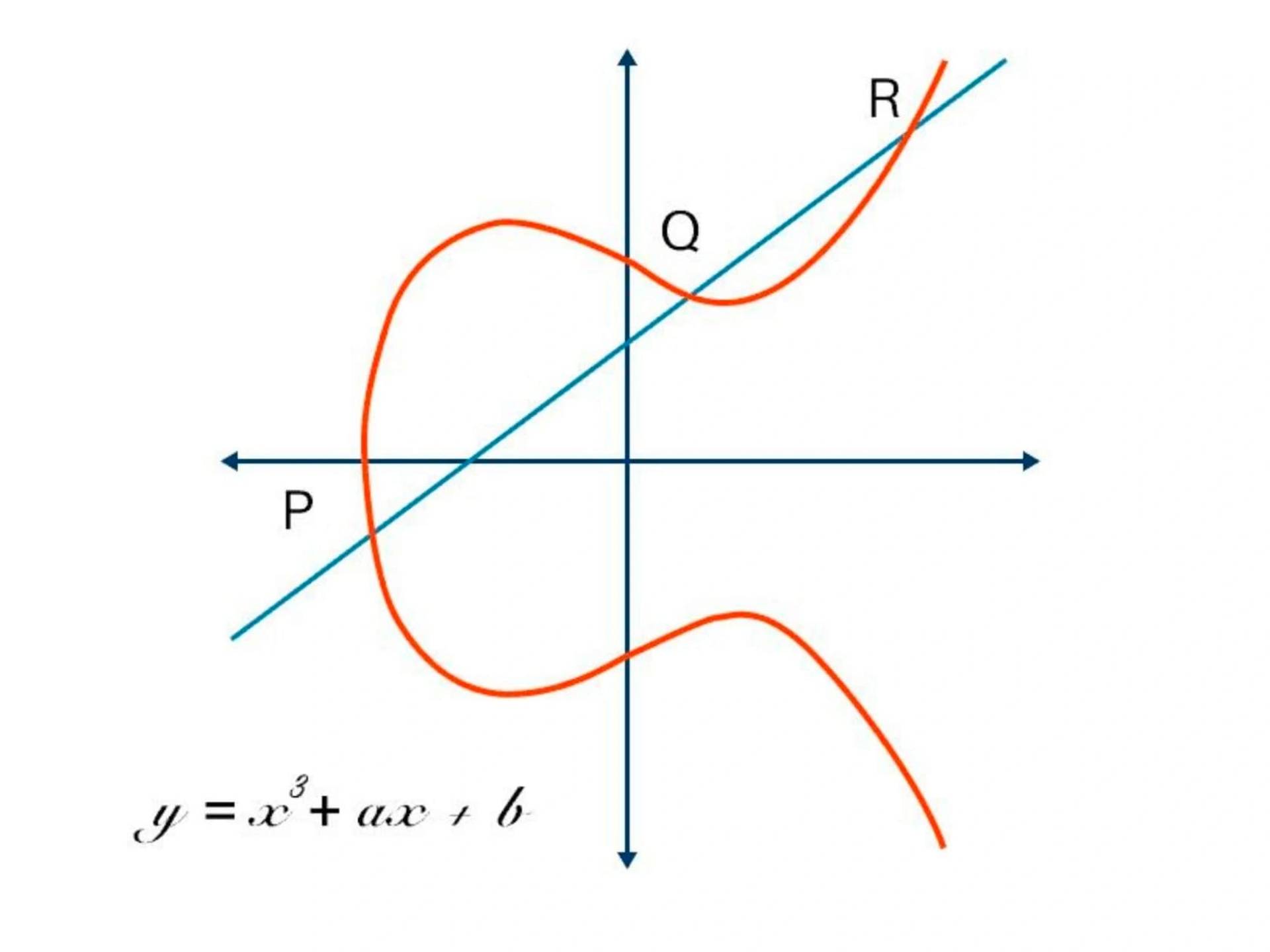
在 RSA 和 Diffie-Hellman 引入之后，研究人员探索了其他基于数学的密码学解决方案，寻找除分解之外的其他算法，这些算法可以作为良好的陷门函数。 1985 年，基于一个被称为椭圆曲线的深奥数学分支，提出了密码学算法。 椭圆曲线是满足特定数学方程的点集，看起来有点像侧放的 Lululemon 标志。

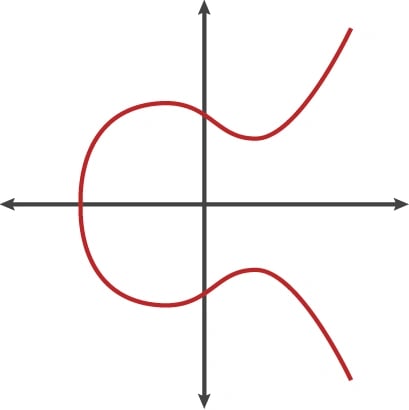
还有其他椭圆曲线的表示形式，但从技术上讲，椭圆曲线是满足一个方程的点集，该方程在两个变量中，其中一个变量的次数为 2，另一个变量的次数为 3。椭圆曲线具有一些使其成为密码学良好设置的属性。^[4]

创建者

Neal Koblitz 和 Victor Miller 独立地共同发现了椭圆曲线密码学，它是当今互联网上实现加密通信的数学的一部分。 在 2019 年接受 All About Circuits (AAC) 采访时，Koblitz 博士说：^[1]

"改变我对数论的看法的是 1977 年左右 RSA 密码学 (Rivest-Shamir-Adleman) 的发明。这是数论在计算机安全中的第一个重要应用。" "椭圆曲线密码学的想法出现在 1984 年。我和其他几个人收到了一份预印本，一个相当初步的版本，是 Hendrik Lenstra 开发的用于分解大整数的算法。如果这个算法足够快，它可能会对 RSA 密码学构成威胁。"