방향성 비순환 그래프(DAG)는 방향성 에지로 연결된 노드로 구성된 그래프 데이터 구조의 한 유형으로, 에지는 특정 방향을 가지며 사이클을 형성하지 않습니다. 방향성 사이클이 없는 방향성 그래프입니다.

DAG의 각 노드는 하나 이상의 들어오는 에지와 하나 이상의 나가는 에지를 가질 수 있습니다. DAG의 에지는 노드 간의 종속성을 나타내며, 에지의 방향은 종속성의 방향을 나타냅니다. 예를 들어 노드 A가 노드 B로 나가는 에지를 가지는 경우 노드 A는 노드 B에 의존한다는 의미입니다.

개요

방향성 비순환 그래프(DAG)는 블록 기반 구조를 사용하지 않는다는 점에서 블록체인과 다릅니다. 대신 트랜잭션은 그래프의 정점으로 표시되고 이전 트랜잭션에 연결됩니다. 노드는 트랜잭션을 검증하고 DAG에 추가하며, 트랜잭션을 제출하려면 작업 증명 작업을 완료해야 합니다. ^[1]

DAG 기반 네트워크에서 새로운 트랜잭션은 블록체인의 블록이 이전 블록을 참조하는 방식과 유사하게 수락되려면 이전 트랜잭션을 참조해야 합니다. 트랜잭션을 참조하면 확인되고, 트랜잭션이 완전히 확인되려면 후속 트랜잭션에서 참조해야 합니다. ^[1]

DAG는 블록 생성의 부재와 채굴자가 없기 때문에 트랜잭션 수수료가 없어 트랜잭션 속도가 빠르며 환경적 이점을 가질 수 있습니다. ^[2]

DAG는 블록체인, 작업 증명 및 지분 증명의 개념과 방향성 비순환 그래프를 사용한 최장 체인 규칙을 결합하여 더 높은 처리량을 허용한다는 점에서 블록체인보다 우수합니다.

역사

DAG의 첫 번째 사용은 날짜가 지정되지 않았지만 그 개념은 매우 유용하여 인간 존재의 새벽까지 거슬러 올라갑니다.

1736년 레온하르트 오일러의 '쾨니히스베르크의 일곱 다리' 출판물은 그래프 이론을 다룬 최초의 논문으로 간주됩니다. 쾨니히스베르크의 일곱 다리는 수학사에서 주목할 만한 문제입니다. 문제는 쾨니히스베르크(현재 러시아 칼리닌그라드)의 일곱 다리를 각각 한 번만 건너는 경로를 찾는 것입니다. 도시 지도를 그래프로 단순화한 후 오일러는 에지, 정점 및 면의 수와 관련된 공식을 도입했습니다.

여기에서 그래프 이론은 수학적 구조로 묘사된 객체 간의 관계 연구로 발전했습니다. 특정 정의를 가진 다양한 유형의 그래프가 있으며 DAG도 그중 하나입니다. ^[3]

사용 사례

가계도

DAG의 원래 사용 사례는 가계도를 만드는 것입니다. 흥미롭게도 그래프 이론에서 트리의 정의에는 대부분의 가계도가 포함되지 않았습니다. 이는 충분히 멀리 뻗어 있는 대부분의 가계도에서 먼 친척이 어느 시점에서 짝짓기를 하여 가족의 부계 및 모계 모두에 공통 조상을 허용하기 때문입니다. 즉, 가계도는 DAG로 간주될 수 있습니다. 각 노드는 사람이고 각 부모-자식 관계는 자손을 가리키는 화살표로 그려집니다. 이것은 아래에 표시된 그래프를 형성하며, 이는 방향성(화살표)이고 비순환적(어떤 사람도 자신의 부모가 될 수 없음)입니다.

DAG로 가계도를 묘사한 것은 고대 로마에서 플리니우스 장로가 로마 귀족 주택의 벽을 장식한 그래프를 묘사한 것으로 기록되었습니다. 이전에는 DAG가 기록되지 않았을 수 있지만 가족사를 설명할 때 자주 설명되었습니다.^[3]

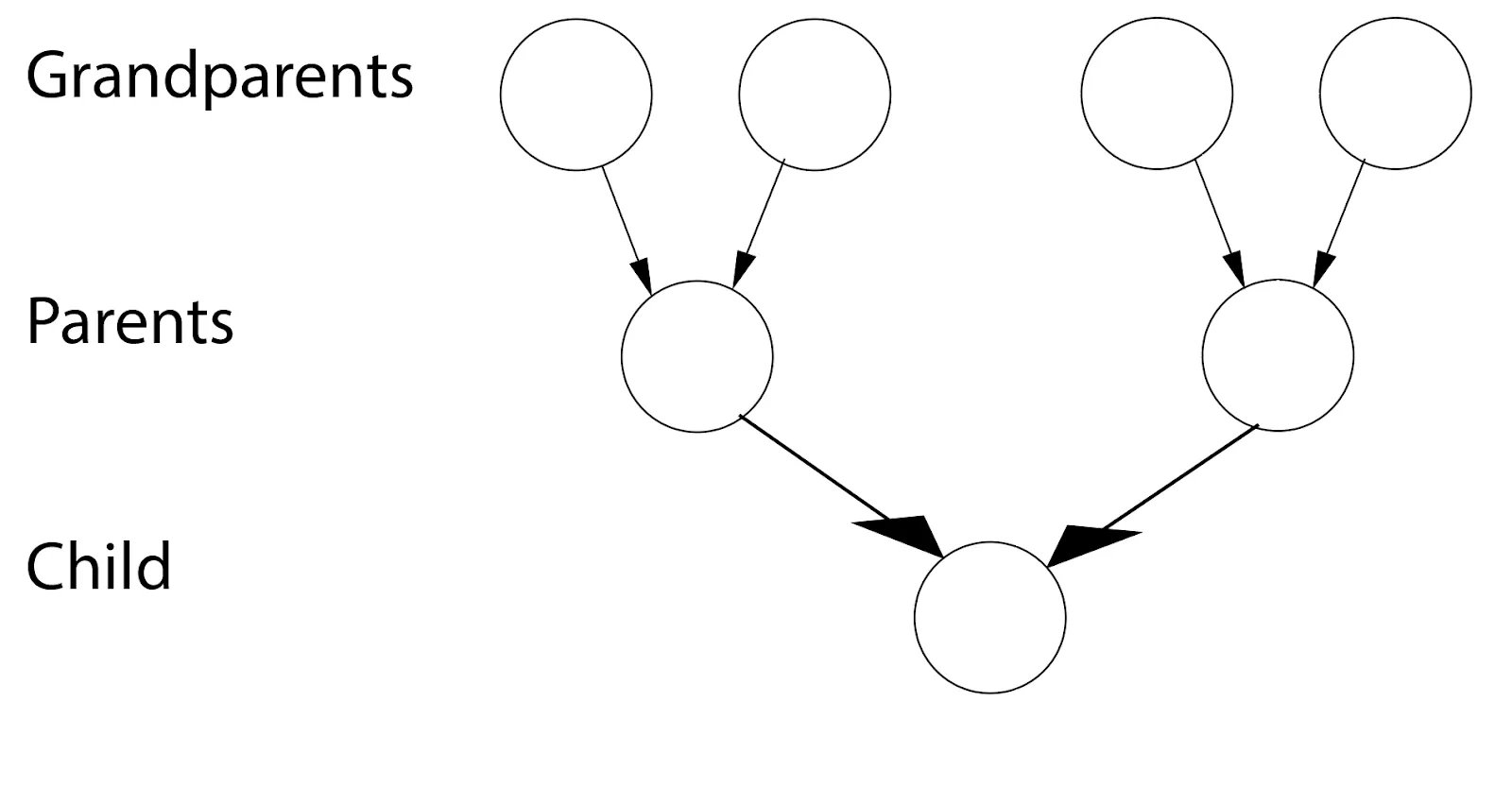
작업 스케줄링

DAG의 또 다른 역사적 사용 사례는 동물과 인간이 DAG를 사용하여 완료할 작업 순서를 파악하는 작업 스케줄링입니다. 일부 작업은 다른 작업이 완료될 때까지 시작할 수 없으며 다른 작업은 언제든지 시작할 수 있습니다. 이것은 그 자체로 DAG입니다.

위의 DAG에서 T1은 저녁 식사를 위해 어떤 동물을 사냥할지 결정하는 것이고, 작업 2는 동물을 사냥하는 것이고, 동시에 수행할 수 있는 작업 3은 장작을 모으는 것입니다. 작업 4는 불을 피우는 것입니다. 작업 5인 동물을 요리하려면 불이 타고 있어야 하고 동물을 사냥해야 하며, 작업 6은 저녁 식사를 먹는 것으로, 먼저 동물을 요리해야 합니다. 피라미드 건설, 로마 설계, 전쟁 중 공격 계획 등과 같은 큰 작업에는 유사한(그러나 더 복잡한) DAG가 사용되었을 것입니다.^[3]

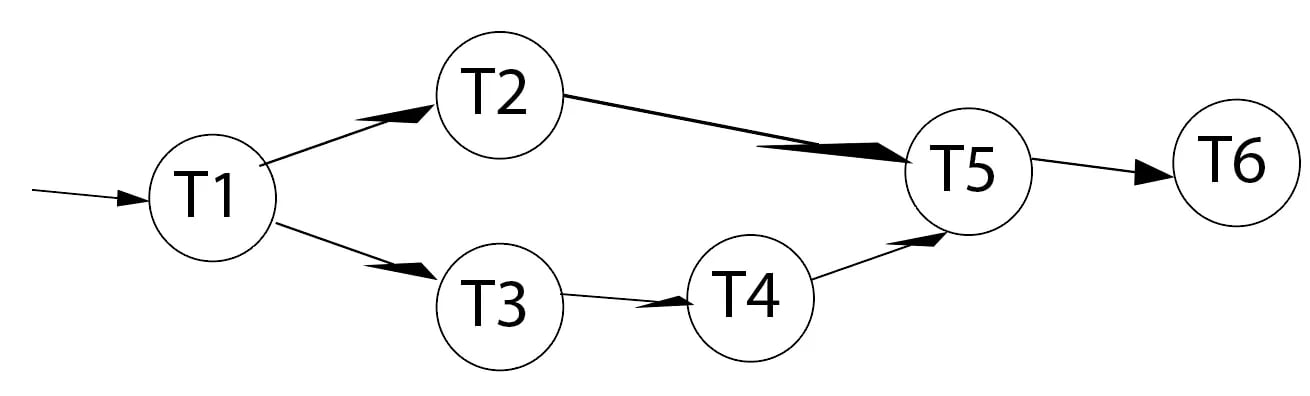
컴퓨터 과학

DAG의 다른 사용 사례는 컴퓨터 과학과 관련된 여러 용도로 더 현대적입니다. 데이터 처리 네트워크, 버전 기록 및 일부 데이터 압축 알고리즘은 모두 DAG를 활용합니다. 그러나 중요한 것은 DAG가 새로운 계시가 아니라 오래된 문제 해결 메커니즘이라는 점입니다. DAG와 블록체인의 병합은 분산 원장 확장성을 위한 큰 도약입니다.^[3]