Elliptic Curve Cryptography (ECC) is a key-based technique for encrypting data famous for being smaller, faster, and more efficient than incumbents. ECC focuses on pairs of public and private keys for decryption and encryption of web traffic. ECC is frequently discussed in the context of the Rivest–Shamir–Adleman (RSA) cryptographic algorithm.

Overview

There are two main different types of encryptions - symmetric encryption, which uses one key to both encrypt and decrypt (e.g. AES), and asymmetric encryption, which uses two different keys (e.g. RSA). These are often called a public and private key, where the private key is not to be disclosed.
RSA uses integer factorization cryptography based on algebraic number theory, while elliptic curve cryptography (ECC) uses integer factorization cryptography based on elliptic curves.
Elliptic Curve Cryptography is a choice for public-key-cryptography, based on elliptic curves over finite fields.^[2]
ECC is used as the cryptographic key algorithm in Bitcoin because it potentially can save ~90% of the resources used by a similar RSA system.^[3]

RSA vs. ECC

ECC and RSA both generate a public and private key and allow two parties to communicate securely. One advantage to ECC however, is that a 256-bit key in ECC offers about the same security as a 3072-bit key using RSA. ECC allows resource-constrained systems like smartphones, embedded computers, and cryptocurrency networks to use ~10% of the storage space and bandwidth required by RSA.

RSA

Based on the idea that the key that anyone uses to encrypt data can be made public while the key that is used to decrypt your data can be kept private. As such, these systems are known as public key cryptographic systems. The first, and still most widely used of these systems, is known as RSA — named after the initials of the three men who first publicly described the algorithm: Ron Rivest, Adi Shamir and Leonard Adleman.
When both the RSA algorithm and the Diffie-Hellman key exchange algorithm were introduced, these new algorithms were revolutionary because they represented the first viable cryptographic schemes where security was based on the theory of numbers. It was the first to enable secure communication between two parties without a shared secret.
Cryptography went from being about securely transporting secret codebooks around the world to being able to have secure communication between any two parties without worrying about someone listening in on the key exchange.

ECC

After the introduction of RSA and Diffie-Hellman, researchers explored other mathematics-based cryptographic solutions looking for other algorithms beyond factoring that would serve as good Trapdoor Functions.
In 1985, cryptographic algorithms were proposed based on an esoteric branch of mathematics called elliptic curves.
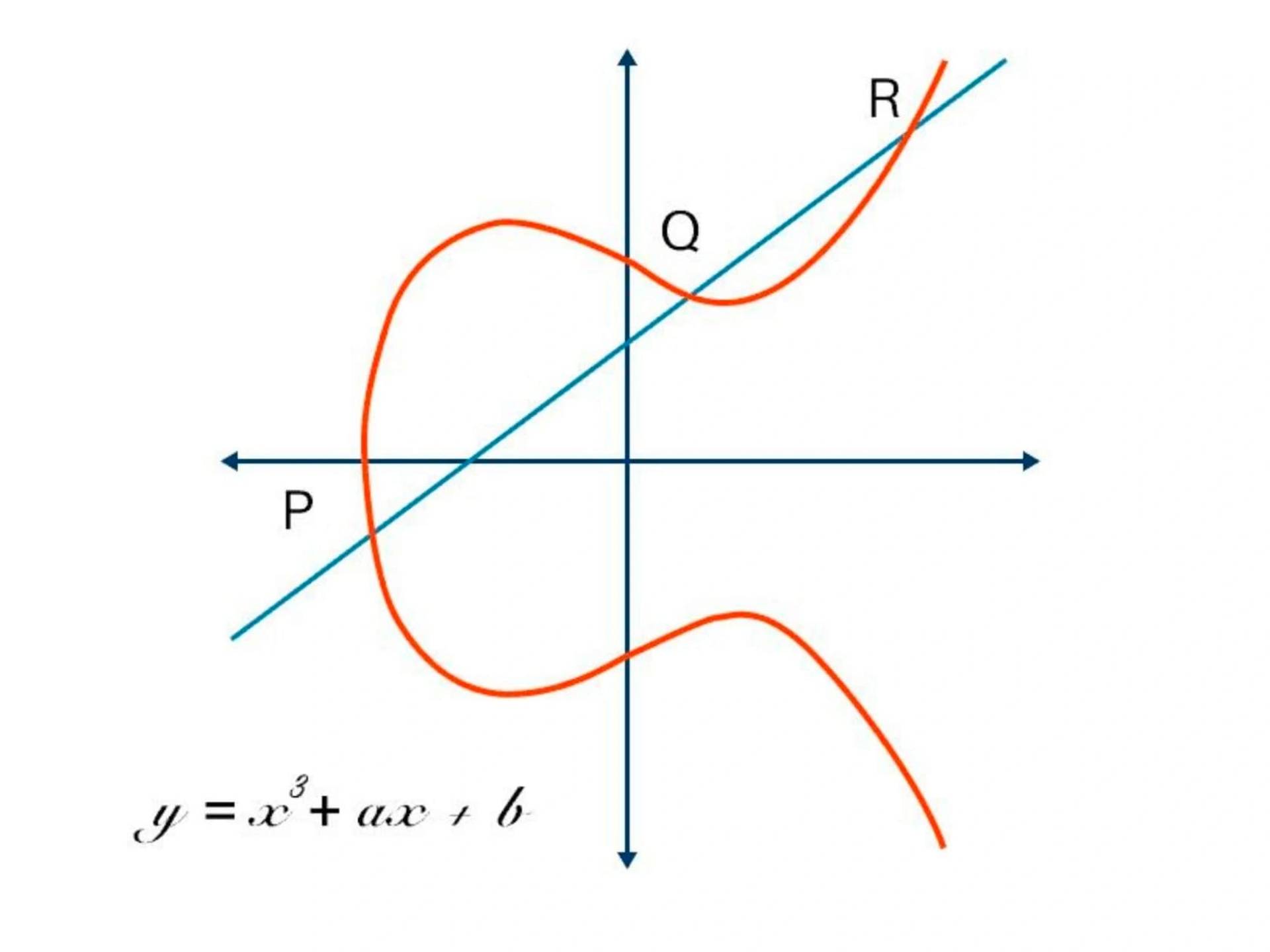
An elliptic curve is the set of points that satisfy a specific mathematical equation, something that looks a bit like the Lululemon logo tipped on its side.

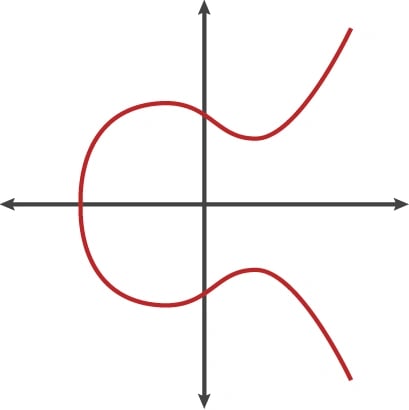
There are other representations of elliptic curves, but technically an elliptic curve is the set points satisfying an equation in two variables with degree two in one of the variables and three in the other. An elliptic curve has some properties that make it a good setting for cryptography.^[4]

Creators

Neal Koblitz and Victor Miller independently co-discovered elliptic-curve cryptography which is part of the mathematics that allows encrypted communication on the internet today.
In an interview with All About Circuits (AAC) in 2019, Dr. Koblitz said:^[1]

"What changed my feeling about number theory was the invention of RSA cryptography (Rivest-Shamir-Adleman) in about 1977. That was the first important application of number theory to computer security."
"The idea of elliptic-curve cryptography came in 1984. I, along with several other people received a pre-print, a rather preliminary-version, of an algorithm that Hendrik Lenstra developed to factor large integer numbers. If this algorithm was sufficiently fast, it could be a threat to RSA cryptography.  "