Read
Edit
History
Notify
Share
Bonding Curve
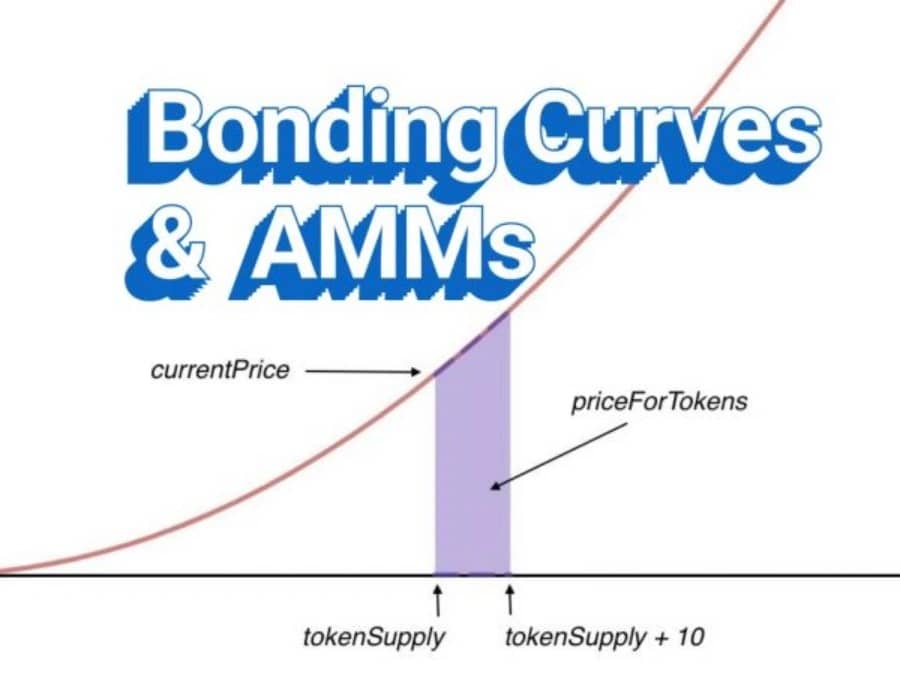
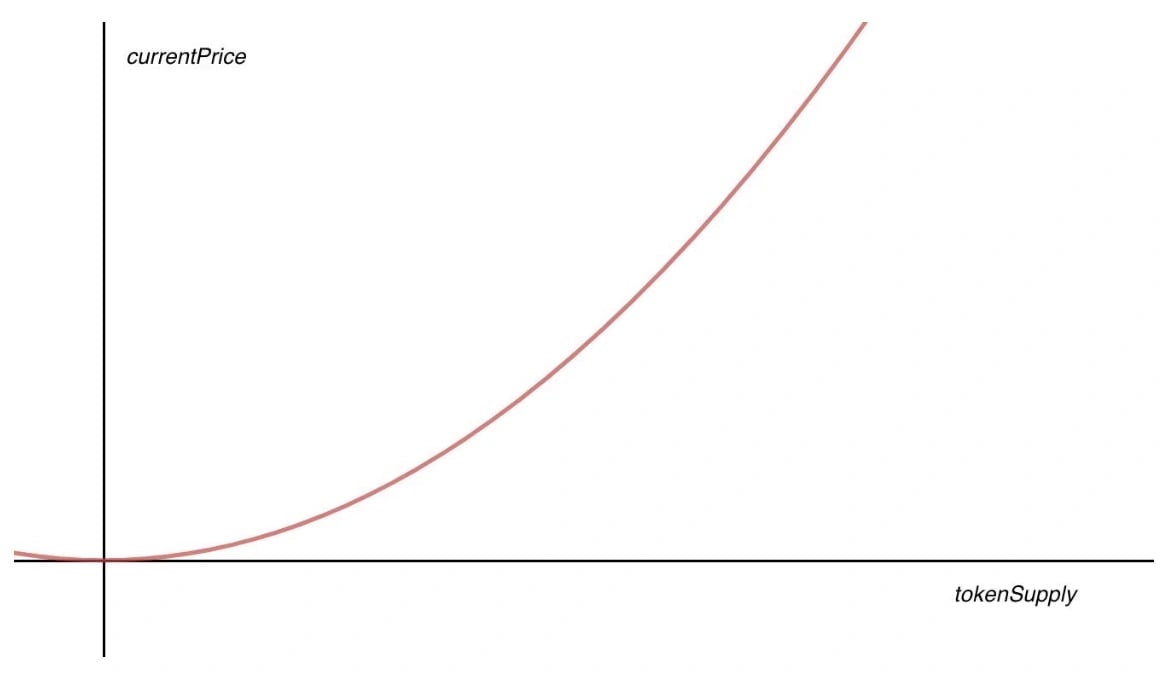
A bonding curve represents a mathematical concept integrated into platforms and applications for computing a token's valuation based on its supply. It is a way of defining the relationship between the price and supply of a particular asset. The bonding curve procedure is about establishing the price of each newly minted token based on the existing supply of the token. [1][2][3]
Overview
The bonding curve fundamentally solidifies the connection between price and supply. It is a mechanism where tokens are acquired at a price specified on the curve using collateral in the form of fiat currencies or other cryptocurrencies. The bonding curve calculates the token's estimated value both when individuals purchase tokens, which results in minting, and when they sell tokens, which leads to token burning. As the bonding curve tokens are minted and burned, the supply fluctuates, which is then reflected in the value indicated by the bonding curve. Since the bonding curve defines a predetermined price at each supply level, it acts as an automated market maker (AMM) for the token at every price level. [1][2][3][4]
History
The concept of bonding curves originated independently in various corners of the crypto space and operated under multiple names during the initial months of its existence—“Smart Tokens” as per Bancor, “Curation Markets” within Simon De La Rouviere's circles, and “Bonding Curves” as coined by the Zap Protocol. [12]
[15]
In August 2016, Bancor conceptualized the design for Smart Tokens but publicly announced the token concept on February 14, 2017. In September 2017, the Zap Oracles team introduced the concept of bonding curves, while Simon de la Rouviere, a developer at ConsenSys, popularized the initial idea of bonding curves when considering how to retain "social liquidity" in an increasingly automated world. Bonding curves were part of a larger set of designs within curation markets, a model that enables groups to more effectively coordinate and earn from the value they co-create around shared goals—an initiative that Rouviere was actively working on. [13][14]
Initially, the Zap Oracles team drew inspiration from curation markets and distilled the core token model. Curation markets, featuring a protocol design where a token can be continuously minted based on a price set by the smart contract, influenced the design principle of bonding curves. Rouviere noted that the continuous token model, following a similar approach as Bancor’s smart tokens, was conceived and published at the beginning of March 2017 under the initial name “Bonded Curation Community.” Today, the terms Bonding Curves, Smart Tokens, Continuous Tokens, and Curation Markets are broadly used interchangeably, particularly in the context of Automated Market Makers (AMMs), ICOs, continuous organizations, and continuous token-curated registries.
[12][13][16]
Bancor's Smart Tokens
Bancor's strategy involved employing smart tokens as AMMs to initiate the development of low-liquidity markets and order books. Their rationale was that newly introduced tokens often faced challenges in drawing sufficient market participants to establish a fluid and robust exchange of value where buyers are readily matched with sellers and vice versa. This presented a significant obstacle to token trading, essentially constituting a chicken-and-egg problem for new tokens. By leveraging bonding curves, users have the capability to purchase or sell tokens through the bonding curve, even in scenarios with limited or no other buyers or sellers in the market. [12]
Bonding Curves and Curation Markets
Bonding curves are applicable in curation markets. In this model, tokens generated through bonding curves are employed to establish a staking and reputation system for content curation. Participants in these curation markets stake their tokens to endorse content they find valuable. As the quality of their curations improves, it is probable that more users will be drawn to purchase the token and vote on content deemed more valuable. [12]
Benefits
A bonding curve can serve various purposes which are: [10]
Token value
Bonding curves have the potential to generate intrinsic value for a token, ensuring that tokens can be redeemed at the existing price on the curve, establishing an inherent price floor. [10]
Liquidity and continuous trading
Bonding curves play a pivotal role in providing liquidity by establishing a market for tokens, enabling them to be bought or sold at any time. This liquidity feature is crucial for new projects aiming to establish a vibrant ecosystem, as bonding curves ensure continuous liquidity. Acting as a market maker, the bonding curve eliminates the need for buyers and sellers to wait for a counterparty to initiate a trade. [10][11]
Price determination and predictability
In contrast to fixed-price models, bonding curves empower token prices to adjust based on market demand, promoting stability by discouraging speculation and emphasizing utility. The predetermined and unchangeable shape of the bonding curve adds an extra layer of price predictability, allowing participants to anticipate how alterations in supply will impact the price. [10][11]
Decentralization
Bonding curves offer an optimal method for projects to distribute tokens in a decentralized manner. Users can obtain tokens through direct interaction with smart contracts, diminishing the dependence on centralized exchanges. [11]
Examples
Friend.tech
Friend.tech is a decentralized social media platform that aims to redefine how people engage with content, interact with influencers, and gauge the worth of insights. It is designed to attract crypto enthusiasts seeking engagement with Crypto Twitter (now X) figures while allowing individuals to tokenize themselves and “marketize” their online identity. [11][17][18]
Friend.tech employs objective quantification through market dynamics and utilizes bonding curves to simplify the market dynamics associated with social profiles. Every interaction on the platform translates into tangible value, distinctly represented in share prices. This encompasses activities such as original content creation, shared trading strategies, discovered airdrops, or meticulously curated information within private chats. Individual share prices serve as a barometer, reflecting the value of each user based on the quality of their contributions. In the case of Friend.tech, the price of a share in ETH follows a mathematical relationship with the supply of shares within a given group. Therefore, the more shares purchased, the higher the likelihood of price increases. [11][17][19]
Hashmasks
Hashmasks is a digital art project by Suum Cuique Labs. The platform enables users to acquire a non-fungible token (NFT), representing one of the 16,000 artistic works, with the potential to reveal valuable rarity when a Hashmasks is randomly purchased. Hashmasks utilize a bonding curve-type pricing model. In this case, it employs a piecewise bonding curve, where minting a new Hashmasks becomes progressively more expensive in successive tiers as the number of tokens increases. [11][20][21]
Fei
Fei, a decentralized finance (DeFi) protocol, is designed to establish a fully decentralized stablecoin. Utilizing bonding curves, the platform facilitates the circulation of its native token, FEI, through sales. Users can acquire FEI during surges in demand by purchasing on the bonding curve. The price function starts at a low point to reward early adopters, and the protocol supports the creation of bonding curves denominated in ERC-20 as well as a single curve denominated in ETH. [11][22]
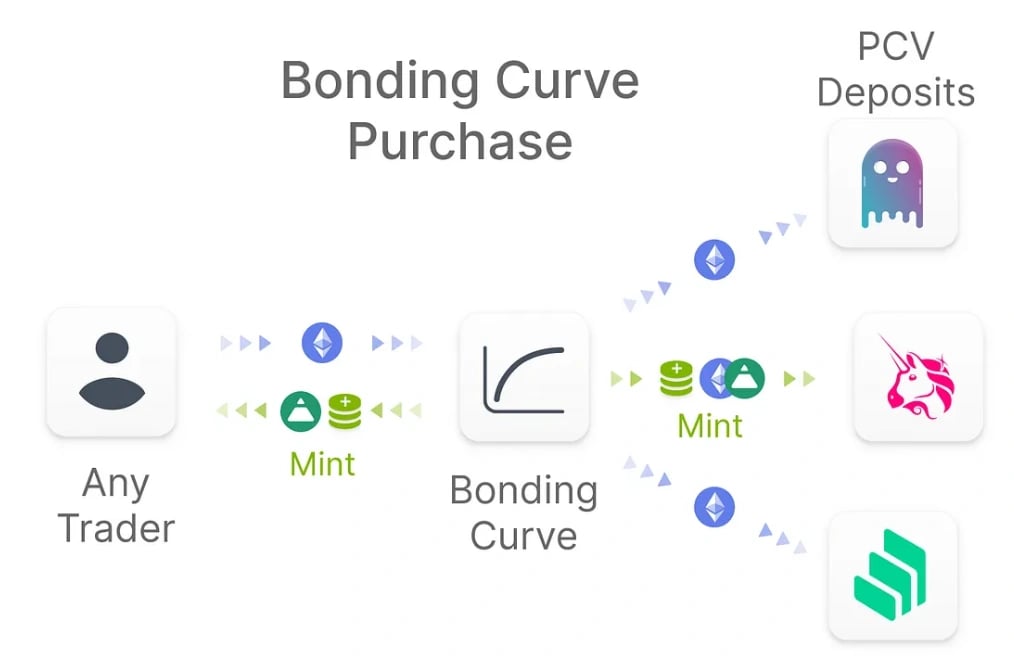
The purchase of FEI through a bonding curve with the deployment of ETH as a Protocol Controlled Value (PCV) [22]
As the curve approaches and fixes at the $1 peg, the ETH bonding curve has a target FEI supply for bootstrapping before fixing the price at $1. This target is known as Scale, signifying the conclusion of the bootstrapping phase upon reaching it. Notably, users cannot sell FEI directly on the bonding curve; instead, the protocol retains incoming ETH as PCV. The Fei Protocol deploys PCV to create a liquid secondary market, allowing users to sell FEI back into ETH. [22]
Bonding Curve
Commit Info
Feedback
Average Rating
How was your experience?
Give this wiki a quick rating to let us know!
Media
REFERENCES
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
[14]
[15]
[16]
[17]
[18]
[19]
[20]
[21]
[22]